Gravitational-wave detectors sensitivity limits
Like for any detectors, the sensitivity of gravitational-wave detectors is greatly affected by the signal-to-noise ratio. As such, minimizing the noise is a core subject in the improvement of gravitational-wave detectors. If we take a look at the current major noises present in Virgo we can highlight some points:
-
The Quantum noise is dominant at high frequencies.
-
At low frequencies, the noise contribution is diverse.
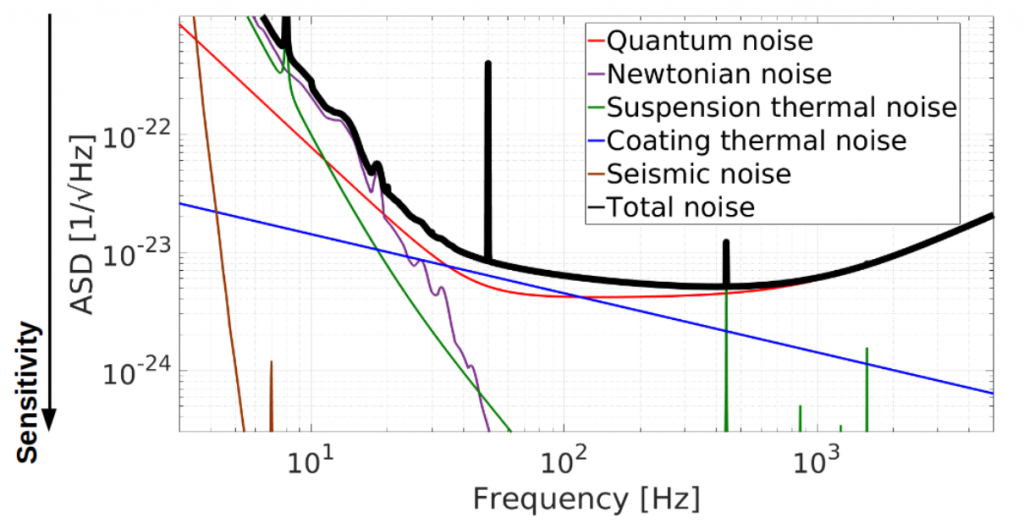
As upgrades are made and all kinds of technical noise are reduced, the contribution of quantum noise in the Virgo sensitivity curve will only increase if no improvements on this part are made as well.
Quantum noise and squeezed light
Quantum noise stems from the quantum nature of light: photons – light quanta – follow a Poisson distribution during their propagation which affects the gravitational-wave detector.
This effect is mainly visible in 2 ways, depending on which element sees this randomness:
-
The radiation pressure noise when interacting with the interferometer arm’s mirror: photons push the mirror which modifies the arm length.
-
The shot noise when interacting with the photo-detector: the detector sees signal variations from the photon random time delay.
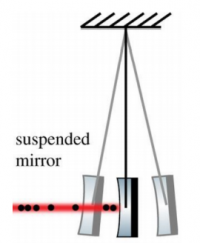

For these 2 effects, the level of noise depends on the laser parameters, notably the uncertainty in amplitude (for the radiation pressure noise) and the uncertainty in phase (for the shot noise).
If one tries to plot the classical state of laser light in the Amplitude/Phase domain, one obtains a round spot whose diameter indicates the uncertainty of the amplitude and phase of the light.
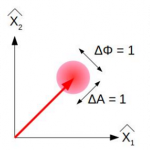
Using the notation of this graph, the Heisenberg uncertainty relation will be as follows:
ΔA ΔΦ ≥ 1
Squeezed light is a special state of light where the amplitude uncertainty or the phase uncertainty can be improved (meaning reduced) at the price of a degradation of the other (still following the Heisenberg uncertainty).
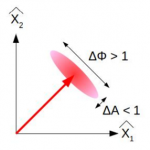
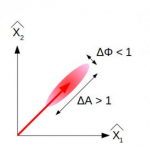
This means that using this special kind of light state, we can reduce one of the 2 noises composing the quantum noise at the cost of increasing the other.
An additional optical cavity allows introducing a transition between amplitude squeezing and phase squeezing around a controlled frequency, which is matched to the parameters of the gravitational-wave detector in order to reduce quantum noise on the whole frequency range.









